如何設計出一種精妙絕倫的證明遞歸方案

前言：在 zkRollup 以及 zkEVM 賽道所遇到的幾乎所有難題，其本質都是算法問題。ZKP 硬體加速之所以屢屢被提及，主要原因是當下算法普遍較慢。為了避免落入「算法不夠，硬體來湊」的尷尬境地，我們應該從本質算法上解決問題。設計出一種精妙絕倫的遞證明方案是解決這個問題的關鍵。

隨著智能合約的不斷發展，越來越多的 web3 應用逐步問世，以太坊等傳統 Layer1 交易量迅速攀升並隨時可能發生擁堵。如何在保證能獲取 Layer1 提供的安全性的同時獲得更高的效率成為了亟需解決的問題。

對於以太坊而言，zkRollup 使用零知識證明算法作為底層構件，將原本需要在 Layer1 上執行的高昂的計算搬到鏈下，並向鏈上提供執行正確性的證明。該賽道主要有 StarkWare、zkSync、Scroll 以及 Fox Tech 等項目。

事實上，在 zkRollup 的設計中，對於效率有很着高的要求：希望提交的證明值足夠的小，這樣可以減輕 Layer1 的計算量。而為了獲取足夠小的證明長度，各個 zkRollup 項目都在改進算法以及架構設計，例如 Fox 就結合了最新的零知識證明算法開發了自己的證明算法 FOAKS，來獲得最優的證明時間和證明長度。

此外，在驗證證明的階段，最平凡的手段是線性的生成證明並依次驗證。為了提高效率，大家首先想到的是多個證明打包成一個證明，這也就是通常提到的證明聚合（Proof Aggregation）。

直觀來講，對於 zkEVM 生成的證明進行驗證是一個線性的過程，驗證者（Verifier）需要依次驗證每一個生成的證明值。但是這種驗證方式的效率比較低，通訊開銷也比較大，對於 zkRollup 的場景，更高的驗證者端的開銷就意味著更多的 Layer1 層的計算，也就會導致更高的 Gas fee。

我們先看一個例子：Alice 想要向全世界證明自己在本月的 1 號至 7 號都去了 Fox 公園。為此，她可以分別在 1 號至 7 號的每一天都拿着當天的報紙在公園拍一張照片，這 7 張照片打包就成為一個證明。

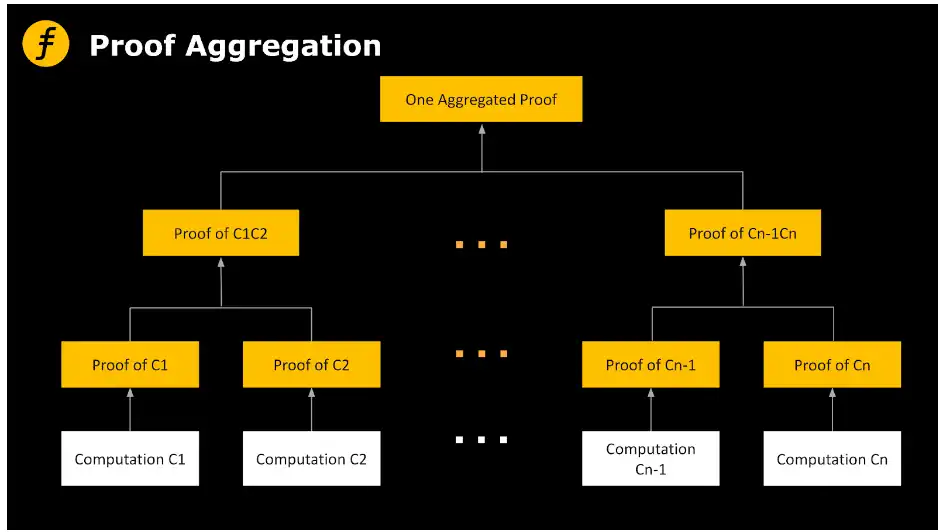
上面例子裡把 7 張照片直接放入一個信封就是直觀意義上的證明聚合，這在實際情況中對應的是將不同證明連接在一起並依次線性驗證，即先驗證第一個證明，再驗證第二個證明以及隨後的證明。問題是這種做法既不會改變證明的大小，也不會改變證明的時間，與一個一個去證明並驗證的效果一樣。如果要實現對數級別的空間壓縮，那就要使用下面提到的遞歸證明（Proof Recursion）。

Halo2 以及 STARK 所用證明遞歸方案

為了更好的說明什麼是遞歸證明，我們回到上面的例子。

Alice 的 7 張照片實際上是 7 個證明。現在考慮將它們合併起來，於是 Alice 可以在 1 號拍好照片，在 2 號拿着這張照片和 2 號的報紙拍照片，在 3 號再拿着 2 號拍的照片和 3 號的報紙拍照片。以此類推，Alice 在 7 號拿着 6 號的照片和 7 號的報紙拍下最後一張照片，而其他小夥伴在看到 7 號的這最後一張照片，就可以驗證在 1～7 號 Alice 都去了公園。可以看到，之前的七張證明照片，被壓縮成了一張。而在這個過程中的一個關鍵技巧，即是「包含照片的照片」，相當於將之前的照片以遞歸的形式嵌套進了之後的照片當中。這跟把很多照片放一起再拍個照片是不同的。

zkRollup 的遞歸證明技巧可以大幅壓縮證明大小。具體來講，每一筆交易都會生成一個證明，我們設原始的交易計算電路為 C0，P0 為 C0 的正確性證明，V0 為驗證 P0 的計算過程，證明者（Prover）將 V0 也轉化為對應的電路，記作 C0』。此時，對於另一筆交易的證明計算過程 C1，就可以將 C0』和 C1 的電路合併，這樣一來，一旦驗證了合併後的電路的正確性證明 P1，就相當於同時驗證了以上兩筆交易的正確性，也就是實現了壓縮。

而回顧上述過程可以發現，其實壓縮的原理在於將驗證證明的過程又轉化為了電路，然後生成「對於證明的證明」，所以從這個角度來說，是一種可以不斷向下遞歸的操作，因此也被成為遞歸證明。

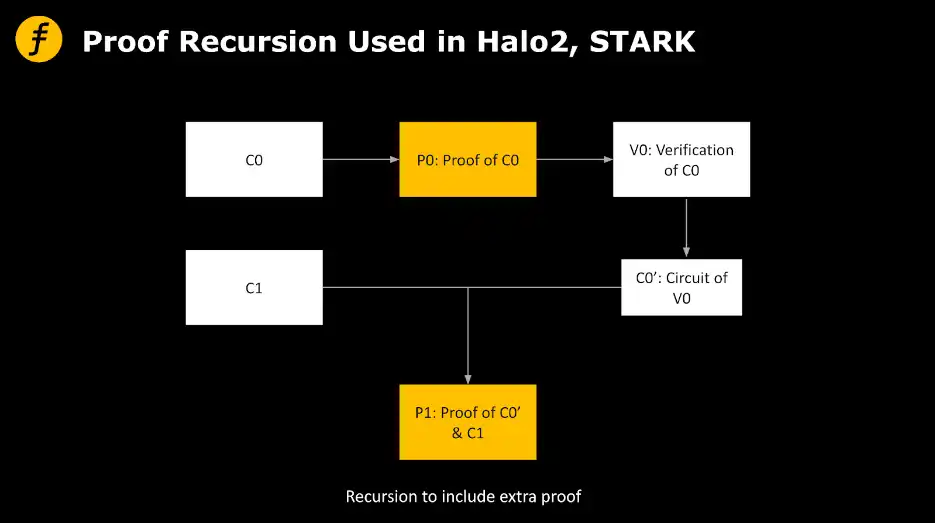
Halo2 與 STARK 所採用的 Proof Recursion 方案能夠並行生成證明，並將多個證明進行合併，使得驗證一個證明值的同時可以驗證多個交易執行的正確性，那就能夠壓縮計算的開銷，從而極大的提高系統的效率。

然而，這樣的優化仍然停留在具體的零知識證明算法之上的層次，為了進一步提高效率，我們需要更底層的優化和創新，Fox 設計的 FOAKS 算法通過將遞歸的思想應用在一個證明的內部做到了這點。

FOAKS 所使用的證明遞歸方案

在 Fox Tech 是一個 zkEVM-based 的 zkRollup 項目。在它的證明系統中，同樣使用遞歸證明的技巧，但是內涵與上述遞歸方式有不同之處，主要的區別是 Fox 是在一個證明的內部使用了遞歸 (Recursion) 的思想。為了表達出 Fox 所使用的遞歸證明的那種不斷將要證明的問題約化，直到約化後的問題足夠簡單的核心思想，我們需要再舉一個例子。

在上面的例子，Alice 通過拍照證明自己在某天去了 Fox 公園，於是 Bob 提出了不同的建議，他認為證明 Alice 去過公園的問題可以被約化為證明 Alice 的手機去過了這個公園，而證明這件事又可以被約化為證明 Alice 手機的定位在公園的範圍里。因此，為了證明 Alice 去過這個公園，她只要在公園的時候用她的手機發送一個定位就行了。如此一來證明的大小就從原本的一張相片 (一個很高維的數據) 變為一個 3 維的數據 (經緯度和時間)，有效的節約了成本。這個例子並不完全恰當，因為也許有人會質疑 Alice 的手機到過 Fox 公園不代表 Alice 本人到過，但是在實際的情況中，這個約化過程是數學形式上嚴格的。

具體而言，Fox 的遞歸證明的用法是在電路層面的遞歸。在進行零知識證明的時候，我們會將要證明的問題編寫成電路，接着通過電路計算出一些需要滿足的等式。而與其展示這些等式是滿足的，我們再次將這些等式編寫成電路，如此往復，直到最後要證明滿足的等式變得足夠簡單，我們便能輕鬆的直接證明了。

從這個過程當中我們可以看出，這麼做更貼近「遞歸」的含義。值得一提的是不是所有算法都可以使用這個遞歸技術，假設每一次遞歸會將複雜度為 O(n) 的證明變為一個 O(f(n)) 的證明，而這個遞歸過程本身的計算複雜度是 O(g(n))，則遞歸一次後總計算複雜度就變為 O1(n)=O(f(n))+O(g(n))，兩次後就是 O2(n)=O(f(f(n)))+O(g(n))+O(g(f(n)))，三次後就是 O3(n)=O(f(f(f(n))))+O(g(n))+O(g(f(n)))+O(g(f(f(n))))，...，以此類推。因此，只有在 f 和 g 兩個對應算法特性的函數滿足對某個 k 有 Ok(n)

原文連結