電腦是如何下棋的：深入了解人工智能(3)

主流的國際象棋程序往往採用一種比較“保守”的局勢篩選策略，搭配一種比較“激進”的信息匯總策略。而主流的圍棋程序則正好相反，在局勢篩選方面相當“大膽”，卻對從這些局勢變化收集來的信息的使用相當“謹慎”。這主要是由於目前對這兩種棋類的盤面靜態評估的質量不同導致的。

對於國際象棋，已經找到了一種在“很多情況”下可以既快速又相對準確地對盤面進行靜態評估的方法——當遇到這類“大致可以進行靜態評估”的盤面時，這個靜態評估方法有相當的可信度，而對於其他情況的盤面卻完全不起作用。由於擁有這樣一個具有“部分可靠性”的靜態評估，國際象棋程序的策略“從概念上”可以理解為是對從當前盤面出發的每一種可能的變化都不停向前展開，直到遇到一個可以大致靜態評估的盤面或者超出了一個預定的“最大展開步數”為止。這樣的“保守”選擇策略使得計算機對於一定階段之內的所有變化都有了大致評估。接下來計算機在“假設”這些評估是正確的前提下，計算按照完美下法哪一種變化是最優的。

根據硬件計算能力，計算機還會設定一個“最小展開步數”，即使一個變化在展開不到最小步數時就遇到了一個“比較好評估的局面”，系統依然會繼續往前看，而不會就此停止。這是為了最大限度地彌補“對比較好評估的局面進行靜態評估時依然有可能出錯”的缺陷。在開發第一個人類大師級水平的計算機“Belle”的過程中，人們發現弈棋計算機的最小展開步數越大，其棋力越強。也就是，原則上只要通過不斷增強硬件的計算能力，國際象棋機器就可以通過看得越來越深而下得越來越好。

1997年的“深藍”計算機在配備了400多塊專門設計的硬件加速卡之后，獲得了每秒鐘展開並評估2億次盤面的恐怖計算能力，歷史上第一次代表機器戰勝了人類國際象棋冠軍。在隨后的十幾年裏，按照“摩爾定律”增長的計算機硬件能力變得愈加強大，計算機又先后多次戰勝人類國際象棋冠軍。越來越多的人相信，機器在國際象棋領域早已超越了人類的弈棋能力。

然而，計算機能夠戰勝人類國際象棋冠軍並不全靠超強的硬件計算能力，軟件算法方面的持續改進同樣必不可少，甚至影響更大。

比如上面提到，國際象棋系統在“概念上”窮盡了一定步數之內的所有變化。但在真實的弈棋計算機中，一系列優化算法使得系統在不完全展開某些變化的同時也能夠得到和完全展開一樣(或類似)的效果。這樣節省下來的時間可以用於把已知變化“看得更深”，從而極大提高了系統在“概念上”的等效計算能力。

其中最經典的例子是由人工智能先驅約翰·麥卡錫提出的////剪枝法，它巧妙利用了“國際象棋是雙人零和游戲”的特點，以最優的方式避免所有不必要的變化展開。

零和游戲

又稱零和博弈(Zero-Sum Game)，是博弈論中的一個概念，指游戲(博弈)雙方是競爭而不是合作關係，或者是一種“你死我活”的狀態。例如兩人對弈，一方贏，另一方必然是輸，不存在“雙贏”。贏棋得1分，輸棋減1分，兩人得分之和就總是0，所以稱為零和游戲。

根據計算機科學家唐納德·克努特(Donald Knuth)的數學分析，在理想情況下，αβ剪枝法僅需評估所有b^d個變化中的b^(d/2)個，就可以保證得到和評估所有b^d個變化完全一樣的結果。換句話，我們需要增加 倍硬件計算能力才能使動態評估加深一步，而使用αβ剪枝法則可以使動態評估輕鬆增加整整一倍的“思考深度”*2！

αβ剪枝法成型於20世紀60年代，是國際象棋弈棋的諸多優化算法裏最經典的一種。如今的國際象棋程序中還使用了大量其他優化方法，使得實際的動態評估過程遠遠比簡單的“枚舉”要高效得多，只是“從概念上”，它們從評估質量上等效(或接近)於一次對未來若幹步內所有局勢變化的窮舉展開而已。

國際象棋的動態評估方法(或其變種)也廣泛應用於大多數其他棋類的對弈系統，其中很多達到或超越了人類冠軍的水平。然而，這套思路卻在圍棋博弈中遭遇了滑鐵盧。截至目前，沒有一個基於國際象棋的動態評估思路的圍棋系統可以超過人類業餘入門級水平。很多人把這一失敗歸因於圍棋比國際象棋更大的計算複雜度(這當然看起來是最明顯的原因之一)。

但是，根據許峰雄博士在2007年發表的那篇名為“Cracking GO”(破解圍棋)的文章，在擁有接近國際象棋的靜態評估質量的前提下，我們完全可以在軟件和硬件兩方面進行一系列優化，使得國際象棋的動態評估方法在圍棋中也達到類似的思考深度。如果我們假設圍棋大師們的智力並不顯著高於國際象棋大師的話，這樣的思考深度也許會使機器在圍棋上再次戰勝人類。也就是，對於當今的硬件能力，圍棋的複雜度並不是不可逾越的鴻溝。那麼，到底是什麼原因導致國際象棋的策略無法適用於圍棋呢？

筆者的觀點是，“窮舉型” 策略////3至今未在圍棋中廣泛應用，更大的障礙恐怕還是缺少一個像國際象棋那樣能夠對於“一大類”盤面進行“大致準確的評估”的方法。前面介紹靜態評估方法的部分已經提到了，目前圍棋盤面的靜態評估方法一般只在棋局前期黑白雙方尚未“短兵相接”時有一定效果。當棋局進入關鍵的中盤廝殺之后，如果仍然使用現有的靜態評估方法，我們就會發現：在達到硬件計算能力可承受的最大預判步數時，大部分棋局變化都處於不能“大致準確評估”的狀態。基於這些十分不“靠譜”的評估結果去考慮所謂“完美”走法，得到的結果自然也是不大靠譜的。

正是由於缺少“靠譜”的靜態評估方法，目前所有頂級圍棋程序轉而採取一種比較“謹慎”的信息匯總策略。

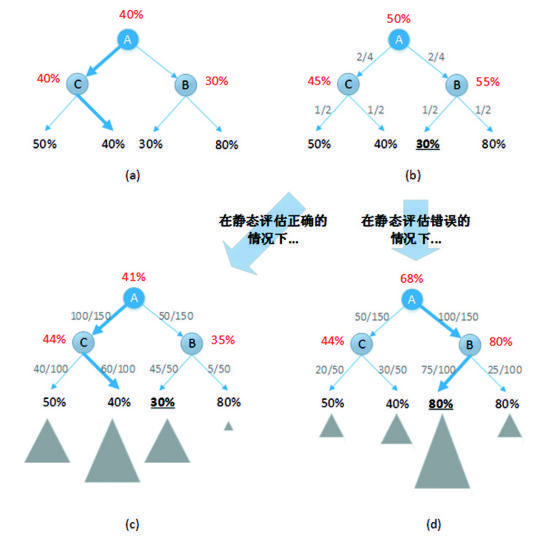
在國際象棋中，如果一個盤面有兩種走法，一個估計勝率30%，另一個估計勝率80%(如圖(a)中盤面B所示)，計算機會傾向於相信這些結果都是大概“靠譜”的，因此該盤面自身的勝率應該等於所有走法中的最優結果(我方盤面取最大值，對手盤面取最小值)，因此認為盤面B的勝率是30%。這是一種比較“激進”的信息匯總策略：當發現了30%勝率的走法時，系統會完全丟棄80%勝率的走法所帶來的信息，選擇全部相信30%勝率的走法。

而在圍棋程序中，計算機認為對每個盤面的直接靜態評估結果都是不可靠的，但是相信“對該盤面下所有走法的全部評估結果”卻整體上仍然對該盤面的勝率具有指向性。現有圍棋程序一般採用對所有評估結果進行加權平均的方式來體現這種指向性，其中“權重”基於對當前評估結果的可信度進行設定。舉例來。在圖(b)中，假設對盤面B下兩種走法所直接導致的盤面進行靜態評估的結果勝率分別為30%和80%，而盤面C下的兩種走法勝率分別為50%和40%。因為這4個估計值可能都存在偏差，所以我們並不偏信其中任何一個；另一方面，在偏差沒有系統性地倒向“某一類盤面”或“某一類走法”的前提下，我們有理由相信這4個盤面評估結果具有相同的可信度(或“不可信度”)，因此應該具有相同的權重。所以在只知道這4個靜態評估結果的情況下，我們認為盤面B的評估勝率是0.5×30%+0.5×80%=55%，盤面C的評估勝率是0.5×50%+0.5×40%=45%。同時，這樣做出的對B和C的判斷自身仍然有可能存在偏差，所以在以盤面B和C為基礎再評估盤面A時也要考慮到這一點，因此A的評估結果同樣是B和C的結果的再次加權平均0.5×45%+0.5×55%=50%。

我們看到，這樣根據等權重得到的對A的評估結果實際上是綜合了所有當前已知信息之后給出的一個“模棱兩可”的評估。考慮到“已知信息”本質上的低可靠度，這也許就是我們在這種情況下“應該”得到的答案。當然，這樣一個僅僅基於4次靜態評估的結果並不是計算機給出的最終答案。對於一個給定盤面，我們考察的變化越多，獲取的信息量也越大，因此對這個盤面的評估值也傾向於更可靠，從而這個評估值在參與加權平均時也理應獲得更大的權重。換句話，我們根據對一個盤面“深思熟慮”的程度來量化對其評估結果的“可信度”，認為一個進行大量分析后得到的評估結果在可信度上優於分析較少的評估結果。這就涉及到如何選擇那些需要進一步深思熟慮的變化的問題。

[3]