隨機波動率與期權定價模型淺析

隨機波動率的主要思路是將標的資產價格的波動率描述為一個由價格水平、波動率均值回歸趨勢和波動率方差控制的隨機過程。

a

black-scholes模型

隨機波動率實質上就是跳出了傳統金融市場以一定時期內波動率作為恒定參數考慮市場的框架，而認為波動率本身是隨著價格變化而變化的，這一變化過程符合隨機過程。

在當前的金融市場，因為該類模型考慮的因素更多、理論基礎更為嚴謹而受到不少投資者的關注。

雖然black-scholes模型通過隨機波動率對期權定價（某些寬鬆的假設實質上在交易過程中也是可以被接受的），也將影響期權權力的波動率及分布概率等問題引入到整個評估體系中，但當時還有諸多尚未解決的問題。

其中一個重要的不足之處在於它對於基礎資產價格回報恒定波動率（以及其波動率不受價格變化影響）的假設。這種假設意味著使用期權的對沖者要不斷地對波動率假設進行調整來反映實際的市場價格數據，從而導致了對沖比例的不斷變化。

也導致了傳統期權定價模型無法對隱含波動率的一些固有特性給予合理的解釋。在現實市場中，black-scholes模型給出的期權理論定價也比較難吻合觀察到的期權市場價格。

black-scholes模型根據當前標的價格和靜態波動率來得到當前的期權價格，存在著一些難以克服的缺陷，比如說假設股票價格的收益率是遵循一個固定的均值和方差的正態分布等。

但是在實證中我們發現波動率事實上隨時間變化有一個集聚過程，這與black-scholes模型假設有極大的出入。另外金融界與學術界也意識到金融價格時間序列的分布形態明顯體現出尖峰厚尾的回報特點，也即是說市場的尾部風險較高，這實質上是期權定價中一個明顯的溢價因素，且不能被固定波動率的假設所捕捉。

除此之外，金融價格時間序列中波動率偏離后均值復歸的特點也是black-scholes模型無法刻畫的難點。在期權市場的實際交易中隱含波動率往往呈現波動率微笑形態，隨著執行價格不同位置的變化，期權反推的隱含波動率並不一致。

就波動率本身而言，我們可以由市場數據觀察到它的主要特性包括：波動率簇集（volatility clustering）、回報分布尖峰厚尾（high peak/fat tails）導致的高波動率變化以及波動率均值回歸（volatility mean-reverting）。

其中尖峰厚尾特性是由於有不同方差的分布混合而產生的。顯然，要對期權進行準確的定價，對於波動率隨機過程的刻畫就尤為重要，特別是在非平值期權的定價方面。

出於以上的考慮，我們認為將隨機波動率引入到期權定價當中十分有必要。

隨機波動率的主要思路是將標的資產價格的波動率描述為一個由價格水平、波動率均值回歸趨勢和波動率方差控制的隨機過程。這樣一來就提供了對波動率動態變化進行刻畫的方式，進而也提供了對期權進行更加準確定價的可能。

b

heston模型：刻畫波動率變化的基礎模型

在克服之前所提到的諸多問題方面，目前業界主流的方法是對傳統black-scholes模型的一些拓展，比如說我們知道在已知執行價格、標的價格、到期日的情況下，影響期權價格的主要因素是波動率和利率變化。

所以可以用隨機波動率模型和隨機利率模型刻畫這兩個重要的因子，同時，在考慮波動率分布方面，除了之前提到的諸多特點外，因為它還有跳躍的情況，我們還可以加入隨機波動率跳躍模型。

如此一來，期權的定價實質上轉變為了我們在資產價格、利率水平和風險價格之間平衡的解決方法。為了更加準確地在該框架下以刻畫波動率的思路為期權定價，我們使用隨機波動率模型來優化期權價格的計算。其中一個比較基礎的模型就是heston模型。

heston在1993年提出這種模型，並且提供了期權價格的閉式解。由於可以考慮資產價格和資產波動率的相關性，而且假設資產價格有一個擴散的過程，因此在這個模型中，期權的價格是通過計算看漲期權交割在實值區域的概率得到的。下面簡單介紹一下其邏輯過程：

heston模型假設股票價格s服從擴散分布（幾何布朗運動），其中以μ這個漂移參數作為波動方向的調整。heston和b-s最大的區別是在判定波動率時不再認為其是一個常數，而是也服從一個擴散過程。

在實際操作過程中可以運用伊藤定理來獲得波動率，根據cox、ingersoll、ross三人寫出的隨機偏微分方程，以不同參數分別刻畫波動率均值復歸的速度、波動率長期均值及波動率的波動率。此處模型考慮了加入波動率與回報之間相關性的聯系，以使得波動率影響得以體現，這有賴兩個方程的相關性分析。

相關性參數的刻畫尤為重要，因為它反映了價格變動的偏度，也很大程度上顯示了價格回報尖峰厚尾的特點。

當相關性ρ>0時，會導致厚尾右偏：因為當波動率隨回報的變大而變大，會對價格變動起到放大作用。與之相對的，當相關性ρ<0時，會導致價格回報厚尾左偏：因為當波動率隨回報的變大而變小，會對價格變動起到減小作用。

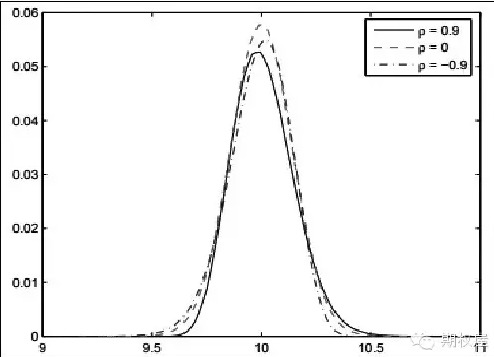
相關性之所以重要，除了上面討論的一些原因，最重要的還是因為波動率變化的精確捕捉，我們可以在不同相關關係背景下為期權找到正確的價格。

在金融市場，特別是股票市場，我們可以觀察到明顯的杠桿效用（leverage）和崩盤恐懼/巨災（crash-ophobia）效應。杠桿作用通常被理解為當股票價值下跌會提升公司的財務杠桿比率，這意味著公司股權資產的風險加大，波動率加劇（回報與波動率正相關）。

而股票價值上升會降低公司的財務杠桿比率，從而降低公司股權資產風險，波動率降低（回報與波動率負相關）。

我們知道black-scholes模型最大的問題之一就是恒定波動率假設不能捕捉的市場資訊過多，也就造成了定價的相應偏差，但是若我們使用heston模型的假設之后，在不同相關性下自然可以刻畫之前期權偏差部分的變化。

在得到波動率與價格變化方程后，在t時刻，歐式期權的價格有剩余交割日（t-t），可以以傳統b-s的交易框架以p1、p2兩個概率概念代替原有的累計概率函數n（d）進行定價分析。p1和p2代表的其實正是我們看漲期權最後實值交割的概率。

計算這里的p值需要反轉計算風險中性機制，最後可以將其表述為一系列復雜的計算公式，但因為閉式解各級參數都有對應公式，需要的投資者可以直接套用。

通過公式的計算，可以得到p1和p2值的閉式解，進而得到看漲期權的理論計算值。有了看漲期權的價格，看跌期權則可以通過call-put parity平價公式來得到。

在heston模型的理論框架下，特別值得注意的一點就是回報分布的偏度、峰度是由波動率與回報的相關性決定的，而傳統black-scholes模型中，波動率為恒定值，所以二者對同樣的執行價格與標的產品定價時勢必產生差別，下圖是假設某資產價格變動及假設波動率與回報相關性分別為-0.5和與0.5時與black-scholes公式定價差異的變化情況。

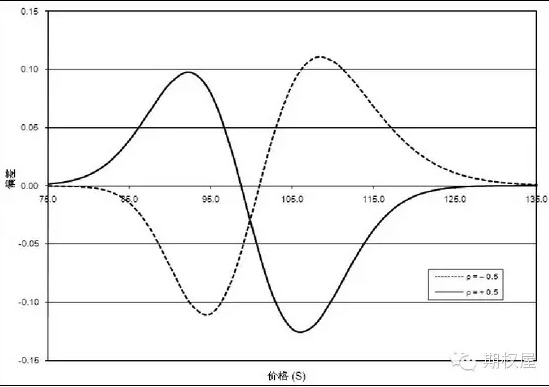
我們發現當波動率與回報假設為正相關時，實值看漲期權若以heston模型定價會比black-scholes模型定價便宜，但若是虛值看漲期權狀態則會比black-scholes模型定價更貴。

若波動率與回報假設為負相關時，實值看漲期權以heston模型定價會比black-scholes模型定價更貴，但若是虛值看漲期權狀態則會比black-scholes模型定價更便宜。

實際上，在現實市場中，我們知道虛值看漲期權的交易價格通常會高於black-scholes模型所給出的價格，這背后有杠桿作用和巨災效用的原因（巨災效用也一定程度被解釋為遠期相對較差流動性的合約會有一定的流動性升水，導致隱含波動率較高）。

與此同時，這樣的特點與回報分布左偏厚尾的特點也較為一致，在相對低執行價格的位置，期權隱含波動率確實應該更高，這也意味著此時波動率與回報應該呈現正相關關係。

所以我們可以認為對看漲期權定價時，當期權為虛值狀態，設置其相關性為正相關，反之為實值狀態時，則設置其相關性為負相關以擬合實際的市場狀況。如此一來，最後我們還能得出符合市場狀況的隱含波動率微笑曲線。

c

heston & nandi模型：波動率歷史記憶性的引入

事實上，盡管heston模型在當前的金融工程領域已經得到了極大的重視，也因為其科學的理論假設得到業界的認可，但是該模型在校準參數與估計的過程中不可避免地會面臨諸多問題，特別是對相關性的估計是一大難點。

因此，業界另一個較為熟知的定價模型heston & nandi也越來越得到金融界人士的認可。其基本思路與t.bollerslev(1986)提出的garch模型有極大的關係。

garch模型是一個專門針對金融數據量體定做的回歸模型，除去和普通回歸模型相同之處，garch對誤差的方差進行了進一步的塑模。在對資產價格變動的刻畫方面，波動率作為最重要的因素之一，一直都是學術與業界研究的重點，而波動率聚簇及自相關的一些特性也開始越來越受到關注。

因此，在對這些特性準確捕捉的諸多模型中，garch模型才成為應用最為廣泛的計量方法。基於對波動率精確的估計與預測，garch的塑模思路得以在heston & nandi模型中對波動率的評估提供重要的參數資訊。

在heston & nandi模型框架下，對於方差的變動是假設服從garch（p，q）過程的，而模型具體參數的推導則又需要從到期日開始往前遞歸來完成。簡單來說，模型的整體思路就是通過garch過程模擬獲得garch參數后，以此為基礎再通過遞歸推出heston & nandi模型的參數，最終確定期權執行概率及期權價格。

通常來講，garch（1，1）比較符合資產價格的波動情況，也具有足夠的顯著性說明問題。與此同時，heston & nandi在其文獻中也證明過隨著到期日長度的增加，garch（1，1）提供的參數所產生的結果會與heston模型的結果趨於一致。

在heston & nandi模型框架下，對數回報應該符合garch（1，1）過程。heston & nandi模型中峰度和方差的確定與garch模型類似，只是在定價過程中，需要預設部分參數以進行遞歸運算。

該模型期權的定價方式與之前heston模型沒有本質上的區別，但是在p的確定方面，heston & nandi模型需要進一步確定模型參數，最終尋得類似heston模型p1、p2的結果進行定價。

d

通過期權的隱含波動率推測其他執行價格的隱含波動率進行期權定價

上文就隨機波動率相關的定價模型進行了討論，不過其定價思路依然有一定的局限性，特別是在參數估計與計算的過程中，這導致模型的理論假設雖較為完備但運用復雜。

所以在期權理論研究的相當長一段時間里，許多學者還就波動率微笑形態的變化進行了大量的工作。其中一個重要的結論在skiadopoulos、hodges和clelow（2000）的論文中有提及，他們將行權價格和價值狀態作為參數，通過pca（主成分分析法）研究了在給定剩余到期時間下標普500指數隱含波動率的變化情況，他們將期權隱含波動率變化形態的研究推上了前臺。

alexander（2001）在此基礎上進一步應用pca對不同行權價期權的隱含波動率與評價隱含波動率的偏離程度變化進行了研究，她的研究結果表明隱含波動率微笑的平行移動、傾斜變化及曲率變化分別占到了波動率方差整體的65%—80%、5%—15%和5%。

這意味著我們在期權定價的過程中，對波動率微笑形態的理解實質上是最為重要的。而對該形態的描繪我們可以參考brown & randall在《if the skew fits》一文中所提及的方法：引入波動率構建函數，使用三項來構成期權價格可使用的波動率形態，分別是平值期權隱含波動率以函數中心的性質確定大致的估計，然后處理對波動率的修正問題。

以tanh非對稱函數體現低執行價格期權高波動率和高執行價格低波動率的特點，其中對偏度影響最大的分項的寬度由指定參數確定，最後，以sech對稱函數來增加隱含波動率在深度實值與深度虛值狀態下的波動率。

如此一來，我們就可以通過流動性較好的期權隱含波動率引入skew的趨勢及skew的程度最終得到修正后的深度實值到深度虛值波動率曲線，最終給各個執行價格期權定價。

該方法也允許我們了解整個期權跨執行價隱含波動率的形態特點，進而解釋65%以上的期權隱含波動率變動。換句話說，當我們擁有一條合理的波動率微笑曲線，則在價格變動時只需要確定平值期權的隱含波動率就可以進而推測其他所有執行價格的隱含波動率，以進行期權定價。

e

隨機波動率類模型引入期權定價方法的展望

本文通過多個貼近市場模型的具體實現提供了一種新的期權定價解決思路，即使市場參與者沒有獲得期權市場價格的渠道，抑或在流動性不夠充裕的情況下，也可以按照標的實時價格通過本文提及的模型計算相對應的期權價格作為參與市場的參考。

最主要的是，考慮到資產價格回報的諸多特點，隨機波動率類模型的引入克服了以往期權定價的諸多不足。

除此之外，隨著業界對期權隱含波動率變化了解的加深，從形狀特點入手解決期權問題的思路也在本文有所提及。

從波動率曲面來看，我們可以通過分析期限結構和波動率偏離來指導我們對市場方向性的判斷，關於波動率曲面的深入研究，不論是對期權本身特性的了解，還是對發現潛在套利機會以及制訂交易規則，都有著重要的意義。

受限於篇幅，本文未就多個模型的推導過程進行介紹，但考慮到模型存在閉式解，投資者可自行直接使用模型框架方面理解。

最後，筆者非常認可george box說過的那句話“基本上，所有的模型都是錯誤的，但有些是有用的”，所以我們不應該癡迷於某種精巧的模型而過分信任甚至夸大其效果，而應該借助模型本身分析了解其推論背后的特點和邏輯幫助我們判斷面臨的情況。

【免責聲明】本文僅代表作者本人觀點，與本網站無關。本網站對文中陳述、觀點判斷保持中立，不對所包含內容的準確性、可靠性或完整性提供任何明示或暗示的保證。請讀者僅作參考，並請自行承擔全部責任。