〈書摘〉用機率看選舉,經濟學家提出「不可能定律」破除完美公平選舉迷思
鉅亨台北資料中心 2019-06-21 17:25

公平的定義到底是甚麼?如何才能在審判或是選舉當中讓參與者心服口服?阿羅的「不可能定律 (Arrow’s Impossibility Theorem)」潑了我們一盆冷水,告訴我們要探討、設計一個理想完美的選舉辦法是不可能的。泛知識時代的 7 堂課,帶你探討論證選舉體制的爭議。
以下內容摘錄自《泛知識時代的 7 堂課》
閱讀時間: 8 分鐘
用機率分析打一場選戰
十八世紀時,法國數學家拉普拉斯 (Pierre-Simon Laplace) 提出用機率的觀念來分析選舉,也就是做決定的過程。他以陪審團的評審制度做為例子,在許多歐美國家的法律審判制度中,有法官審判 (Bench Trial) 和陪審團審判 (Jury Trial) 兩種方式。簡單來說,法官審判是由一位法官聆聽原告和被告提出的證據和理由,做出有罪或無罪的判決;陪審團審判是由若干個陪審員取代法官的職責(雖然往往是先由陪審團做出有罪、無罪的決定,如果有罪,再由法官量刑)。
陪審團通常由七十二個陪審員組成,陪審員都是普通的老百姓,因為陪審團的精神正是由公眾做有罪、無罪的判決。審判的時候,陪審員按照自己的判斷,對被告投下有罪或無罪的票,全體陪審員投票的結果就決定被告的罪名是否成立。重要的關鍵問題是,應該需要多少張有罪或無罪的票才能決定罪名是否成立?
目前美國的陪審團制度一共有十二個陪審員,必須全部一致同意才能決定罪名是否成立;英國的陪審團制度一共有十二個陪審員,必須有十票以上才能決定罪名是否成立;蘇格蘭的陪審團制度一共有十五個陪審員,但是只要八票就足以決定罪名是否成立。美國和英國的陪審制度中,會有陪審團懸而不決 (hung jury) 的可能,這個時候在法律上的程序是複審。蘇格蘭的制度是多數決,因此不會有陪審團懸而不決的可能。
法國數學家康多色提出一個合理且嚴格的標準,真正的勝利者是在所有一對一對決中都獲得勝利的候選人,因此也叫做「康多色勝利者」。其中有幾個有趣的問題:第一,最明顯的問題是,按照選舉人的排序,經過單循環對決後,如果沒有「康多色勝利者」該怎麼辦?我們可以像棒球比賽一樣,讓得分最多的候選人當選;或是和足球比賽相似,在一對一對決的時候,用得票的多寡來做考量。
道奇森倒提出了一個不同的想法:當所有的選舉人都完成排序,計算結果沒有「康多色勝利者」時,我們可以想辦法收買選舉人改變他們的排序。假設收買一個選舉人,在他的排序中交換二個相鄰候選人的位置,價格是一塊錢,需要付出最低價而變成「康多色勝利者」的候選人就獲勝當選。
讓我們看一個例子,四個候選人 A、B、C、D,十一個選舉人的排序分別是:{A, D, C, B}、{A, D, C, B}、{A, B, D, C}、{A, B, D, C}、{B, C, A, D}、{B, C, A, D}、{B, D, C, A}、{C, B, D, A}、{C, B, D, A}、{C, B, D, A}、{D, C, B, A},單循環對決的結果是:
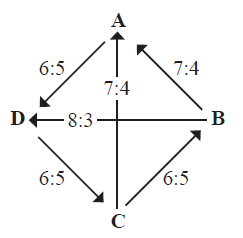
如果第一個選舉人把排序從 {A, D, C, B} 改成 {A, C, D, B},C 就是「康多色勝利者」;如果第十一個候選人把排序從 {D, C, B, A} 改成 {D, B, C, A},B 就是「康多色勝利者」。
但普遍來說,候選人找出如何用最低的價錢收買哪些選舉人,請他們如何改變排序,讓自己變成「康多色勝利者」,站在演算的觀點來說,是相當複雜的一件事,用算法複雜度的語言來說,那是一道 NP 完全 (NP-Complete) 的題目。
許多不同的選舉辦法,再加上其中可能的調整和變化,大家一定覺得每一個選舉辦法都有理由,也包含爭議的地方。不過 1972 年的諾貝爾經濟學獎得主阿羅 (Kenneth Arrow)〔註 15〕,在 1951 年的博士論文中,潑了我們一盆冷水,告訴我們要探討、設計一個理想完美的選舉辦法是不可能的。阿羅博士論文的研究結果,正是他獲得諾貝爾獎的一部分原因。
阿羅的「不可能定律 (Arrow’s Impossibility Theorem)」是這樣說的:首先,假設有三個或三個以上的候選人(因為只有二個候選人的案例比較簡單),有 n 個選舉人,每個選舉人按照自己的判斷進行排序,因此選舉辦法就是如何按照這 n 個選舉人的排序得到結論,也就是選舉的結果。
用社會科學裡簡單的語言來說,社會上的每一分子都有對若干事件重要性的先後排序,例如在政府經費的分配中,教育、醫療、交通、康樂活動的排序,選舉結果就是綜合大家意見的排序。用專家的語言來說,社會上每一分子有其「個人效用函數 (individual utility function)」,選舉就是從所有人的「個人效用函數」求出整個「社會效用函數 (social utility function)」。
舉個簡單的例子來說明這些觀念,假如有三個候選人,八個選舉人,對候選人的排序分別是 {A, B, C}、{A, B, C}、{A, B, C}、{A, B, C}、{A, B, C}、{A, C, B}、{C, A, B}、{C, B, A},用排序決做為選舉辦法,選舉的結果是 {A, B, C};用汰弱留強的選舉辦法,選舉的結果是 {A, C, B}。但是阿羅提出一個選舉辦法必須滿足三個公平合理的標準:
一、 每個選舉人都把 A 排在 B 前面,選舉的結果必須也把 A 排在 B 前面。
二、 每個選舉人都不改變 A 和 B 在排序中的相對位置(A 比 B 高或 B 比 A 高),不管如何改變其他候選人在排序中的位置,選舉的結果,A 和 B 的相對位置都會一樣;換句話說,在選舉的結果中,A 和 B 的相對位置不受其他候選人的位置干擾。
三、 選舉辦法不容許選舉人中有獨裁者,獨裁者的定義是,不管其他選舉人的排序如何改變,選舉的結果一定是一個特定選舉人的排序,直覺來說,第三點是合乎情理的條件。
但是阿羅證明滿足這三個條件的選舉辦法不可能存在!例如選舉的結果可能包含一個三角循環,因此必須剔除某些候選人對決的結果,來打破這些循環;也可能因為加入一個弱不足道的候選人,而改變選舉的結果,這些都違反了阿羅所訂定的標準。雖然我們不可能在這裡證明阿羅的不可能定律,其實他原來的證明只有八頁,有興趣的讀者可以去把這些證明找出來細讀(後來也有人提出不同的證明方法)。
不過我們也不必完全絕望,放棄繼續尋找合乎阿羅三個標準的選舉辦法,讓我舉二個例子,當然這些例子都是調整、改變過阿羅原來設定的條件。
第一個例子是,如果按照阿羅原來的定義,選舉人對候選人的排序沒有任何限制,會產生一個特例:首先,所有候選人有一個「自然」的排列順序,在這個排序中,選舉人指定一個候選人做為首選,接下來在這個排列中,和首選候選人距離愈近的候選人,排序愈高,距離愈遠的候選人,排序愈低。舉個具體的例子,在欣賞音樂的時候,每個人對音量大小有不同的意見,
首先,音量大小有一個自然的排列順序,由最大的音量到最小的音量,選舉人就在這個自然的排列順序中,選出首選的音量,次選比首選音量大一點,三選比首選音量小一點,四選則是再更大一點的音量,五選是再更小一點的音量,這種方式叫做單峰排序 (Single Peak Preference Theory)。當所有選舉人的排序都是單峰排序時,多數決是滿足阿羅三個標準的選舉辦法。
第二個例子是,選舉人不單單把候選人排序,還替他們打分數,例如從 0 到 9;選舉的辦法是,把所有候選人得到的分數加起來,按照總分排列,這叫做得分選舉,雖然滿足了阿羅的三個標準,但是卻超出他原來對選舉方法下的定義,按此定義,選舉人只能對候選人排序,不能打分數。有關阿羅的不可能定律的文獻非常豐富,還有很大的空間值得去探討。
【書籍介紹】

- 書名:泛知識時代的 7 堂課:邁向選舉、密碼、商業交易的新思路
- 出版社:時報
- 出版日期:2019 年 02 月
【作者介紹】
劉炯朗
麻省理工學院電腦博士。
為國際知名的電腦資訊學者,在即時系統、電腦輔助設計、VLSI 布局、組合最佳化、離散數學等領域均有傑出之貢獻,是國際上聲譽卓著的科學家、教育家。曾先後當選中央研究院院士、電子電機工程師學會(IEEE)會士、計算機協會(ACM)會士。
曾任教於麻省理工學院及伊利諾大學,1998 至 2002 年間擔任臺灣國立清華大學校長,作育英才無數。於 1968 年出版之組合數學及 1977 年出版(1985 年再版)之離散數學教科書,被視為經典之作。1973 年發表於 Journal of the ACM 之論文,截至 2019 年被引用達一萬一千餘次,影響極大。
【購書連結】
- 掌握全球財經資訊點我下載APP
上一篇
下一篇